Building Intuition for Lattice-Based Signatures – Part 2: Fiat-Shamir with Aborts
Introduction
This two-part blog series aims to build some intuition for the main techniques that are used to construct lattice-based signatures, focusing in particular on the techniques underlying Falcon and Dilithium, the two lattice-based signature schemes selected for standardization by the National Institute of Standards and Technology (NIST). In part 1 of this two-part blog post (Building Intuition for Lattice-Based Signatures – Part 1: Trapdoor Signatures), we covered how to build lattice-based trapdoor signatures based on the hardness of the Closest Vector Problem (CVP) using the hash-and-sign paradigm, which lies at the core of Falcon.
In this second part, we will describe an alternative construction of lattice-based signatures relying on the hardness of the Shortest Vector Problem (SVP) and the Fiat-Shamir paradigm, which is used as a basis for the signature scheme Dilithium. For a quick refresher on lattice theory and notation that will be used throughout this post, see the Lattice Background section in part 1 of this blog post.
Table of Contents
Constructing Signatures Using Fiat-Shamir and the SVP
Recall that the SVP problem asks to find a short lattice vector of length at most a multiplicative approximation factor
of the length of the shortest (non-zero) vector in the lattice. In order to construct a lattice-based signature scheme based on the SVP
, we focus on a special case of the SVP
problem instantiated on
-ary lattices, known as the Short Integer Solution (SIS) problem. Formally, SIS
can be defined as follows. Given
, find a short
in the
-ary lattice
satisfying
and
. (Note that any norm can be used here. Common choices include the
and
norms.)
The SIS problem lends itself well to constructing cryptographic primitives. If we choose our domain to be a set of short vectors, then we can show the function is in fact a hash function1 which is collision-resistant and one-way.
Indeed, let and suppose we define the hash function
. If we could find a collision
such that
, then
is a solution to the SIS
problem. Indeed, we have that
and, since both
and
are short, we know
is also bounded, with
, and hence is a solution to SIS
.
We will now show how to use this one-way function to construct lattice-based identification schemes and signatures.
Signature Schemes from Identification Schemes
In order to use SIS as the hard problem at the heart of a lattice-based signature scheme, we use a construction based on identification schemes. In general, one can use a one-way function to construct an identification scheme, which can then in turn be used to construct a signature scheme using the Fiat-Shamir transform as follows.
A commit-challenge-response identification protocol can be used for Alice to prove knowledge of some secret information (such as a private key , corresponding to a public key
). It consists of three main steps: First, Alice chooses a random (secret) value
, and computes a commitment to
using a one-way function
, which she sends to Bob. Then, Bob responds to this with a random challenge
. Finally, Alice provides a response combining
,
and the secret key
in such a way that it can be verified using the commitment
and the public key
, but no information about
is leaked.
As an example, suppose Alice wants to prove to Bob that she knows , the discrete logarithm of
. One method of doing so is the Chaum Identification Scheme:

Note that someone impersonating Alice (i.e. someone who does not know ) would be able to return an answer that Bob accepts at most
of the time, as they can either choose a commitment that verifies correctly in the case of
or
(but not both). Repeating this interaction
times (successfully) would thus convice Bob that the person he is interacting with is Alice with probability
. This process can be parallelized, as is done in Schnorr’s Identification Scheme:

The main downside of this process is the requirement for it to be interactive, as it incurs communication costs, and requires Alice to be available when proving her identity.
To avoid those drawbacks, one can use the Fiat-Shamir heuristic – a method to transform an interactive identification scheme such as the ones above to a non-interactive signature scheme. The basic idea is to replace the challenge with the output of a random oracle (in practice, a cryptographic hash function is used instead) that depends on the message and public values.
For the example above, the identification scheme can be adapted to generate Schnorr (non-interactive) signatures as follows:
KeyGen():
1. 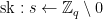 2.
2. 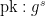 , where
, where 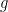 is a public value that generates
is a public value that generates  Sign(
Sign( ,
,  ):
1.
):
1. 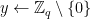 2.
2. 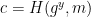 3.
3.  4. Return signature
4. Return signature 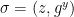 Verify(
Verify( ,
,  ,
, 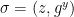 ):
1.
):
1.  2. Output
2. Output 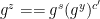
Equivalently, the signer could instead send the signature , in which case the verifier computes
and checks that
to check that it was properly generated.
Lattice-Based Identification Schemes
Taking a similar approach, we can use the one-way function defined using SIS to define lattice-based identification and signature schemes, using an approach first introduced by Lyubashevsky in [Lyu08].
As a first try, we might try to define an identification scheme as follows. First, fix a matrix as part of the protocol parameters. Then, for each iteration of the identification scheme, choose a random bounded
, commit to it by computing the one way function
, and respond to challenges as follows:

Unfortunately, this protocol can leak information about Alice’s secret key. Indeed, since the multiplication and addition step is performed over an infinite group – in particular, over a bounded subset of the infinite group, due to practical limitations – the result cannot be uniformly distributed over the resulting space. In particular, edge values of coordinates of
, such as particularly large or small values or
, leak data about the corresponding coordinates of the secret.
If , signatures risk leaking data about the secret
. Indeed, if any coordinate
of
is equal to
for a given signature, then it must be that
, and hence (since all values are non-negative) that
. On the other hand, if any coordinate
of
is equal to
, we must have that
and
. Similarly, the signature scheme Dilithium chooses
from the set
. In this case, computing
leaks information whenever
is above a particular bound (when
if the parameters are chosen as above).
Additionally, we also cannot modify to never leak information. Indeed, since
is output when
, the distribution of
values that don’t leak information would itself leak information about the secret. For instance, if we modified the sampling process of
so that
is never
for any
such that
(to avoid the leakage of the first case described above), then the fact that some coordinates of
are never
would be discovered when sending the challenge
, and would reveal that those coordinates of the secret
are also
with high probability.
One possible modification to the identification scheme that can be done to avoid this leakage is simply to make the bounds so large that getting a value of that would leak information happens with negligible probability. Unfortunately, this would lead to much larger key and communication sizes, and would correspond to an easier version of the SIS problem.
The solution to this dilemma is straightforward – simply check whether a given would leak information before responding to a challenge. If it would, we simply abort by sending
(which is a special value rejected by the verifier), and try again. If no information would be leaked, we proceed as usual.2
Determining the success probability of a single round can then allow us to determine the expected number of rounds necessary for the verifier to accept with a given probability. It can be shown that this protocol is witness indistinguishable, so these rounds can be performed in parallel, at the cost of some computation and communication overhead.
However, if this new “identification scheme with aborts” is turned into a signature scheme using the Fiat-Shamir heuristic, then we can do better. Indeed, since the “challenge” is generated from the commitment and message using a cryptographic hash function, the signer simply needs to generate new (random) commitments to retry an aborted round of the identification scheme, and repeat until no data is leaked. This process is called “Fiat-Shamir with Aborts”, and allows a signature to have the same size as the communication costs as a single (successful) round of the identification scheme. Putting it all together, we get the following signature scheme:
KeyGen():
1. 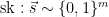 2.
2. 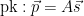 Sign(
Sign( ):
1. Let
):
1. Let  2. While
2. While  :
1. For
:
1. For 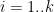 , sample
, sample  , and let
, and let  . Let
. Let  [
[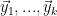 ] and
] and
 [
[ ]
2.
]
2.  3. For
3. For 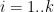 ,
, 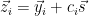 . Let
. Let  [
[ ]
4. If any coordinate
]
4. If any coordinate  is
is 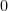 or
or 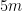 , set
, set  . Otherwise, set
. Otherwise, set 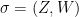 3. Return signature
3. Return signature  Verify(
Verify( ,
,  ):
1.
):
1.  2. For
2. For  , check that
, check that 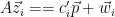 and that all coordinates
and that all coordinates 
The signature scheme Dilithium that has been chosen for standardization by NIST is designed using the above template. As the time required to generate a signature depends on the expected number of iterations, parameters are generally selected so that the expected number of iterations required until a valid signature is generated is relatively small. For example, Dilithium is expected to take between 4 and 7 rounds to output a signature.
In general, lattice signature schemes based on the one-way function are very fast, as matrix-vector multiplications are very efficient operations. However, these schemes generally have very large keys and signatures. This is since each key consists of a vector of
elements, and each signature consists of two matrices of
elements, a commitment matrix
and the matrix
. This results in parameters of a few thousand bytes for public keys and signatures. (In Dilithium, for example, the recommended (optimized) parameters for NIST level III result in a public key size of 1472 bytes, and a signature size of 2701 bytes.) However, there are a number of different optimizations that can be used to reduce the key sizes, possibly at the cost of complexity or of increased computations, which we’ll discuss in the following section.
Options and Optimizations
One straightforward optimization that can be done is to generate the matrix , which is part of a public key, from a seed, using an extendable output function such as SHAKE. This can then be re-computed by the verifier at a relatively low cost, and avoids having the entire matrix
as part of the pubic key. The matrix
can also be defined as a public parameter of a scheme, with each individual key pair simply consisting of the short value
as a secret key, and of
as the public key. However, this requires generating the global parameter
in a trusted method, and, combined with the above optimization, only reduces the size of the public key by the size of the seed, so this optimization is usually not included.
A second common optimization method is to define the lattices over rings or modules. This results in additional structure within the lattices, which can be used to obtain smaller key sizes as well as faster computation speeds. As an example, Dilithium is defined over elements from the polynomial ring , which allows the use of the Number Theoretic Transform (NTT) to speed up matrix-vector multiplications. As a consequence of this change, the signature scheme depends on slightly different security assumptions (the ring/module versions of the existing ones), but these are not currently known to be less secure than their non ring/module counterparts.
Another possible optimization method comes from a modification of the rejection sampling procedure: one can think of the aborts described earlier as a form of rejection sampling with a target uniform distribution. Other target distributions can be used instead, such as a gaussian distribution (or related variant), which allows to minimize the signature size for an equivalent security level, see for example [Lyu11] and [DDLL13]. However, this comes at the cost of additional code complexity, as it requires implementing high-precision gaussian sampling. Hence, some signature schemes, including Dilithium, chose to stick with the standard uniform distribution for rejection sampling for simplicity.
Using a different approach, some additional efficiency can be obtained for an SIS-based signature scheme by introducing a second security assumption, as done by [BG13]. The Learning With Errors (LWE) problem is usually used in lattice-based encryption schemes, and asks to determine the secret when given the pair
, where
is a short error vector. The decisional version of the LWE problem asks to distringuish pairs
from pairs generated from a uniform distribution. However, note that we could instead phrase this as the decisional problem of distinguishing the pairs
from uniformly random pairs, where
and
, since
(and is thus exactly an LWE sample provided
and
are sampled from the appropriate distributions). This allows one to use the same Fiat-Shamir structure to obtain signatures with hardness based on the LWE assumption by modifying the keygen process (in addition to the original hardness assumption of SIS, for technical reasons) – and results in shorter signatures. This optimization is included in Dilithium, and can be seen in their keygen process.
Finally, once the signature framework is fully defined, it is also possible to make additional scheme-specific optimizations or apply compression techniques to minimize the key size. In Dilithium, for example, it was observed that it is possible to compress the signature by omitting some of the low-order bits of some elements in , and instead including a vector of one-bit hints that are used to ensure the result of computations is correct.
Conclusion
The description of lattice-based signature schemes can often seem intimidating at first glance, but at the heart of these schemes are the same constructions used for well-known classical signature schemes, with a few small modifications to adapt these constructions to the case of the infinite groups known as lattices.
Since these first lattice-based schemes, many additional techniques have been introduced to mitigate the various drawbacks of lattice primitives, whether that is the large size of keys and signatures in Fiat-Shamir schemes, or the complexity of implementing secure preimage sampling in hash-and-sign schemes. However, these simple constructions can still be found at the core of modern lattice signature schemes today, and will hopefully help gain an intuition for the working of the more complex constructions that are being standardized.
Many thanks to Paul Bottinelli and Giacomo Pope for their careful review. Any remaining errors are mine alone.
Footnotes
1: This hash function is not suitable for all cryptographic applications; while it is collision resistant and one-way, it is not a fully random function (for instance, , which allows one to infer an underlying structure). While this may be a problem for some applications that require the output of a hash function to be indistinguishable from random, it is also often useful in other settings such as in homomorphic encryption.
2: A similar approach can also works in the classical setting: Girault’s ID scheme [Gir90] is a variant of Schnorr’s identification protocol, but computes the discrete log modulo a composite number and performs the multiplication
over the integers. Security comes from choosing a
in a range much larger than that of
, so no leak occurs with very high probability. In [Lyu08], Lyubashevsky showed that the parameters can be significantly reduced by switching to a variant with aborts.
References
[Falcon]: P. Fouque et al., Falcon: Fast-Fourier Lattice-based Compact Signatures over NTRU, 2020, https://falcon-sign.info/falcon.pdf.
[Dilithium]: S.Bai et al., CRYSTALS-Dilithium Algorithm Specifications and Supporting Documentation (Version 3.1), 2021, https://pq-crystals.org/dilithium/data/dilithium-specification-round3-20210208.pdf.
[Gir90]: M. Girault, An identity-based identification scheme based on discrete logarithms
modulo a composite number, 1990, https://link.springer.com/content/pdf/10.1007/3-540-46877-3_44.pdf.
[Lyu08]: V. Lyubashevsky, Lattice-Based Identification Schemes Secure Under Active Attacks, 2008, https://iacr.org/archive/pkc2008/49390163/49390163.pdf.
[Pei10]: C. Peikert: An Efficient and Parallel Gaussian Sampler for Lattices, 2010, https://eprint.iacr.org/2010/088.pdf.
[Lyu11]: V. Lyubashevsky, Lattice Signatures Without Trapdoors, https://eprint.iacr.org/2011/537.pdf.
[DDLL13]: L. Ducas et al., Lattice Signatures and Bimodal Gaussians, https://eprint.iacr.org/2013/383.pdf.
[BG13]: S. Bai et S. Galbraith, An improved compression technique for signatures based on learning with errors, https://eprint.iacr.org/2013/838.pdf.